Fig 1. Phase-difference measurement and calibration systems: (a) a probe microphone and a strain gauge to detect mouthpiece pressure and lip dynamic strain, respectively, (b) calibration setup to provide a reference of 180° phase difference between pressure and strain signals, and (c) pressure and strain channels for the phase-difference measurement.

A system for measuring the phase difference between the acoustic pressure in a mouthpiece and the vibrational displacement of the upper lip is sketched in Fig. 1 (a) and (c). A strain gauge (Shinkoh type B-FAE-05W-12) was tightly secured to the upper lip by a piece of double-sided adhesive tape (Nichiban, Celtack CW-18). This gauge is very small (0.5 mm long and 1.2 mm wide) and did not disturb the lip's flexibility even when blowing the French horn and trumpet. The gauge treated as an electric resistance is connected by a short lead line to a bridge circuit (Kyowa model DB-120P) which is balanced when no strain is applied. The applied strain is read as an electric voltage, which arises as a departure from the balanced condition. This signal is amplified by a dynamic strain amplifier (Kyowa model DMP-611, with low-pass filtration applied at 1 kHz) and by an additional amplifier (Ithaco model 451). The amplified signal is fed to a 12-bit digitizing waveform recorder (Hewlett-Packard model 5183).
The acoustic pressure in a mouthpiece (or at the input of a pipe without a mouthpiece) is picked up by a probe microphone (Brüel & Kjaer type 4182), which is connected to an amplifier (B&K type 2609). The probe has a length of 25 mm and an internal diameter of 1.24 mm. The amplified signal is then fed to another channel of the above waveform recorder. Finally, both the pressure and the strain signals, which are simultaneously measured, are transformed into phase spectrums in the frequency domain. The phase difference Lp – Lε is obtained by subtracting the phase spectrum of dynamic strain Lε from that of acoustic pressure Lp and reading the value at the sounding frequency.
In advance of the phase-difference measurement in the four acoustical systems mentioned in the Introduction, the applicability of using the strain-detection technique for lip vibration was briefly examined. Human lips are self-excited (or "buzzed") when air is blown over lips which are initially closed. Such self-oscillation of the author's lips was measured with a strain gauge and the following result was obtained: Stable lip vibrations had a fundamental frequency extending from 25 to 48 Hz with a very rich harmonic structure reaching up to the 17th-21st harmonic, where the signal level almost corresponded to the noise level. The dynamic range of our strain measurement system was then estimated as over 40 dB when low-pass filtration was applied at 1 kHz. This result proved the effectiveness of strain detection for measuring the vibration of a brass player's lips.

B. Phase-difference calibration method

The calibration to determine the phase difference between the pressure and strain channels shown in Fig. l(c) was carried out using the setup shown in Fig. 1(b). Such calibration is necessary to define the null phase difference. The same gauge as used for lip-strain detection in Fig. 1(a) was secured to the convex diaphragm at the center of a small dome-shaped loudspeaker (Phillips model 544) in the same manner as explained in Section I A. The acoustic pressure was measured just in front of this diaphragm by using the same probe microphone as shown in Fig. 1(a).
The calibration is based on the assumption that the diaphragm strain and the resulting near-field pressure must be in antiphase. Since the diaphragm may be considered as a simple (or monopole) source in the low-frequency region of interest, the near-field pressure p(r) is proportional to the radial acceleration30 and can be related to the radial displacement ξ of a monopole source according to the equation

p(r) / ξ = –ω2ρS / 4πr,

where r is the distance from the source, S is the area of the source, ω is the angular frequency, and ρ is the air density. It is also a reasonable assumption at low frequencies, where the diaphragm motion is all in-phase, that the internal strain is proportional to radial displacement. From these assumptions it is supposed that the diaphragm strain and the resulting near-field pressure is in antiphase.
Therefore the setup of Fig. 1(b) establishes a reference of 180° phase difference between the pressure and strain signals. The phase difference Φ between the two channels of Fig. 1(c) is thus estimated as

Φ = (Lp – Lε)CAL – 180°,      (1)

where (Lp – Lε) indicates the phase difference measured by the above calibration method based on Fig. l(b) and (c).

C. Relation between strain and displacement of the upper lip

We have to determine the relation between the strain and displacement of the upper lip because the calibrated phase difference between the mouthpiece pressure and the lip displacement is required. Such tissue mechanics as developed by Titze and Talkin11 for various vocal-cord configurations is necessary to obtain a quantitative strain-displacement relation for different lip configurations. This is, however, a future problem. At present it is enough if we have the phase relation when the instrument is sounding.
Let us assume that the upper lip consists of a mass and a spring whose upper end is fixed at a position corresponding to the mouthpiece rim. This lip spring is compressed as well as stretched; the lip mass experiences a restoring force when the lip is displaced from its equilibrium position. When the spring is compressed, the lips tend to open with a positive (upward or outward) displacement of the upper lip. Such a compressed spring gives rise to a negative strain on the lip boundary. When the spring is stretched, the lips tend to close with a negative displacement of the upper lip. Such a stretched spring gives rise to a positive strain on the lip boundary. Consequently, we may infer that the strain and displacement of the upper lip are in antiphase. Also, if one considers the buzzing, one can understand that the lower lip assists this antiphase relation. When the upper lip collides with the lower lip, an external impulsive pressure from the lower lip gives the upper lip a negative stress as well as a positive displacement to make the lips open just after the collision. Since a negative stress on the lip boundary gives a negative strain, the above-mentioned antiphase relation is encouraged. As the upper lip separates from the lower lip, the lip dynamics will be controlled by the internal restoring force. The antiphase relationship is still a hypothesis which needs further refinements.
Hence we have the following relation:

(Lp – Lξ)MEAS = (Lp – Lε)MEAS – 180°,       (2)

where ξ and ε are the lip displacement and strain, respectively. Also, ( )MEAS denotes the value obtained by the measurement system consisting of Fig. l(a) and (c). True phase difference is thus derived from Eqs. (1) and (2) as follows:

Lp – Lξ = (Lp – Lξ)MEAS – Φ = (Lp – Lε)MEAS – (Lp – Lε)CAL       (3)

The values of (Lp – Lε)CAL define a curve of " null phase difference," whose examples will be shown in Section I D.
A few comments should be made in connection with our strain-detection method and lip behavior. According to Martin,4 upward and outward motions of the upper lip are almost in-phase and form an opening. Moreover, the area of lip opening is approximately proportional to the central separation which is mainly due to the upward motion of the upper lip. Hence we may consider that the upward motion is more significant than the outward motion. This is also understood from the comparison between Figs. 4 and 5 in Ref. 4. In fact, larger output signals were obtained from a strain gauge when it was secured to a deeper position of the upper lip. However, such a gauge was inclined to come off because of the moisture in the mouth and the air flow along the lip surface. So the gauge was secured to a proper position, not too deep, not too shallow, so that it can last at least a few hours for the experiment. Such a gauge secured to a proper position can be well seen in a mirror when making embouchure to blow the instruments. Therefore the strain gauge can detect the outward motion as well as the upward motion, although the ratio of the sensitivities to these motions is not known. Also, the upper lip is considered as the primary vibrator,4,31,32 particularly at higher frequencies.

FIG. 2. Phase difference between the acoustic pressure and the dynamic strain in the calibration system consisting of Fig. l(b) and (c) . Left ordinate axis and upper abscissa range (from 100 to 450 Hz) refer to gauges Bl and B2. Right ordinate axis and lower abscissa range (from 280 to 315 Hz) refer to gauge A.

D. Curve of null phase difference

The measured results of (Lp – Lε)CAL, which defines the null phase difference used to evaluate (Lp – Lξ) according to Eq. (3), are shown in Fig. 2. The responses of gauges Bl and B2, which include additional 77-cm and 60-cm lead lines, respectively, were measured with the system described in Section I A. On the other hand, the response of gauge A, which includes an approximately 100-cm lead line, was measured with another system consisting of a hand-made bridge circuit, an amplifier (Ithaco model 451), and a band-pass filter (NF model FV-625A) whose bandwidth was set at 100 Hz. Also, a small electret microphone was used instead of a probe microphone for the phase-difference measurement system with gauge A. This relatively rough system was applied to a lip-driven pipe without a mouthpiece,8 whose experimental result is described in Section II A.
The calibration curves for gauges B1 and B2 shown in Fig. 2 indicate that the phase difference between the pressure and strain channels has the same frequency dependence, although the cause of small discrepancy in magnitude between them is not specified. A very fine lead line (28 mm long) which comes out from the gauge itself is not so strong, and was sometimes broken by the stress between the mouthpiece rim and the upper lip. On that occasion the broken gauge was replaced by a new one, but the measurement of (Lp – Lε)CAL was not repeated. The three curves in Fig. 2 are used to define null phase difference in Section II.

II. EXPERIMENTAL RESULTS

A. Resonant pipe without a mouthpiece

FIG. 3. Phase difference (Lp – Lε)MEAS in lip-driven pipes without a mouthpiece: (a) pipe 1, with gauge A, (b) pipe 3, with gauge B2. Symbol •: relatively thin upper lip stretched sideways, o: relatively relaxed and pro­truded upper lip.

The self-oscillation of two different resonant cylindrical pipes directly blown without a mouthpiece was investigated several years ago.8 Pipe 1 was 282 mm long with an inner diameter of 30 mm, while pipe 2 was 400 mm long with an inner diameter of 37 mm. At that time a simpler measurement system with gauge A was used (see Sec I D). The acoustic pressure in an acrylic resin (Plexiglas) pipe was picked up by a small wall- embedded electret microphone which was located about 15 mm from the upper lip. Later the same experiment was repeated using a third pipe, pipe 3 (286 mm long, 25 mm in inner diameter), and using the measurement system with gauge B2 (described in Section I A) to reconfirm the previous results.
Figure 3(a) and (b) shows the results on pipe 1 and pipe 3, respectively. The experimental data distribution in Fig. 3(a) clearly divides into two groups : one group has lower frequencies and positive phase differences [we are considering Lp – Lξ in Eq. (3)]; the other has higher frequencies and negative phase differences. A very similar result was derived from the larger pipe 2. On the other hand, Fig. 3(b) almost consists of only one group with positive phase differences. The group of negative phase differences may support the outward-striking lip model, while the group of positive ones does not support it, but it does suggest a one-mass upward-striking lip model.33
Higher sounding frequencies, which are apt to give negative phase differences, were produced by stretching the lips tightly and making the upper lip taut and thin (cf. symbol • in Fig. 3). However, lower frequencies, which are apt to give positive phase differences, were produced by relaxing the lips and protruding the upper lip (cf. symbol o in Fig. 3). The embouchure depends on the lip flexibility, which in turn depends on the diameter of the pipe where it is pressed against the lips. This diameter influences vibrational freedom. Such interrelation is assumed to be complex and subtle because the difference between Fig. 3(a) and (b) comes from a small difference in pipe diameter between pipe 1 and pipe 3.
Since the analysis of this interrelation is difficult, we have to restrict our conclusions to the following: Experiments with the larger pipes (1 and 2) support both the outward-striking and the upward-striking lip models ; the smaller pipe (3) hardly supports the outward-striking lip model. The validity of this judgment and our phase-difference measurement method described in Section I will be reconfirmed from the relation between the sounding frequency and the passive resonant frequency in Section III B.

B. Non resonant tube with a mouthpiece

Many brass players carry a tube to quietly practice buzzing and lip control in a mouthpiece. Figure 4 shows this practice tube with a French horn mouthpiece (Lawson S660) as well as a strain gauge, a bridge circuit, a probe microphone, and resonant tubes with a mouthpiece (see Section II C) The practice tube consists of the first 18 cm of taper of a standard French horn lead pipe attached to a short capped cylindrical tube with a large side hole. By adjusting the size of the hole opening, a player can control the "resistance" during practice. This tube cancels all playable harmonics, but allows enough feedback to give the player a feeling similar to that of his instrument. In this sense this tube is nonresonant 28,29 and thus can be used to examine lip behavior in a mouthpiece over a wide frequency range.
The experimental result of Fig. 5 indicates that the phase difference Lp – Lξ of Eq. (3) has negative values of –10° to –40° except for a few data points. Owing to the non resonant characteristic of the mouthpiece-tube system, the sounding frequency varies over a wide range from 250 to 445 Hz instead of over the narrow range shown in Fig. 3 for the lip-driven resonant pipe. Similar results were also obtained by using a trumpet mouthpiece (Bach 5C) instead of a French horn mouthpiece. The negative values of the phase difference suggest that the upper lip is operating in an outward-striking mode in a mouthpiece-non-resonant tube system.

C. Resonant tube with a mouthpiece

FIG. 4. Mouthpiece-non resonant tube and mouthpiece-resonant tube systems, (a) French horn mouthpiece (Lawson S660), (b) non resonant practice tube, (c) strain gauge, (d) bridge circuit, (e) probe microphone, (f) trumpet mouthpiece (Bach 5C), (g) resonant tube Rl, and (h) resonant tube R2. FIG. 5. Phase difference between the mouthpiece acoustic pressure p and the lip strain ε when a mouthpiece-non resonant tube system shown in Fig. 4 is blown. o: Measured data for an end capped tube. •: Measured data for a tube without an end cap. Gauge Bl was used for strain detection. FIG. 6. Measured phase difference between the mouthpiece acoustic pressure p and the player's lip strain ε when the following acoustical systems are blown: o, trumpet mouthpiece-resonant tube Rl system, •, French horn mouthpiece-resonant tube Rl system, and ♦, French horn mouthpiece-resonant tube R2 system. Gauge B2 was used for strain detection.

Since the experimental results from the mouthpiece-non resonant tube system seem to reflect only the behavior of the buzzing lips without significant acoustic feedback, additional experiments on a mouthpiece-resonant tube system are necessary.
Two kinds of tube were made of brass (see Fig. 4): Tube Rl was 350 mm long with an inner diameter of 7.0 mm except for a 15-mm mouthpiece side with an inner diameter of 7.8 mm; tube R2 is 300 mm long with an inner diameter of 21 mm except for a 41-mm mouthpiece side in which inner geometry changes from cylindrical (15 mm long, 7.8 mm in inner diameter) to truncated conical (26 mm long). These tubes are well fitted to a French horn mouthpiece. Since a trumpet mouthpiece is thicker than a French horn one, a proper joint is inserted between a trumpet mouthpiece and the tube.
The experimental results of Fig. 6 indicate that all of three couples (trumpet mouthpiece-tube R1, French horn mouthpiece-tube R1, and French horn mouthpiece-tube R2) have negative phase differences Lp – Lξ ranging from about –20° to about –70°. This suggests that the outward-striking lip model is realized even in mouthpiece-resonant tube systems. Moreover, as described in Section III B, the calculated resonant frequency of the mouthpiece-resonant tube system is clearly lower than the sounding frequency shown in Fig. 6. This frequency relation endorses the reliability of the phase relation of Fig. 6 and confirms the predominance of the outward-striking lip model. However, it should be noted that the experimental result is restricted only to the fundamental mode because the excitation of higher modes was quite difficult.
Also, it should be noted that mouthpiece-resonant tube systems have a much wider resonance frequency band than lip-driven pipes without a mouthpiece. The resonant bandwidth of the former is 30-40 Hz as shown in Fig. 6, while that of the latter is about 10 Hz as shown in Fig. 3. Such a wide resonant bandwidth is possibly due to the coupling between the cavities of the mouthpiece cup and player's mouth. This coupling may happen because the resistance and inertance of lip opening are negligible for the low-frequency, first-mode excitation.5,24 See Section III B for more detailed discussions.

D. Trumpet and French horn

Figure 7 shows the experimental results of a trumpet (Yamaha student model 2320E with Bach 5C mouthpiece) and a French horn (Alexander 103 with a Lawson S660 mouthpiece). The trumpet was blown by the author who had no experience playing the trumpet before this experiment, during which he tried various different embouchures. He could not play a tone higher than fifth mode. Also, it was difficult for him to control loudness, so data points shown by the symbol ♦ in Fig. 7 have tone loudness around mf. On the other hand, the French horn was blown by a semiprofessional player with over ten years' playing experience in symphony orchestras. No special requirement on embouchure was given to him for the experiment, so he played his instrument naturally after several minutes of getting used to an upper lip equipped with a strain gauge. A requirement on tone loudness was given during the experiment. Data points shown by the symbol o indicate the loudness below mp; those shown by symbol • the loudness above mf.
According to Fig. 7, phase difference Lp – Lξ between the mouthpiece pressure and the lip displacement becomes positive except for the second mode. Also, except for the 11th mode of the French horn this phase difference increases as higher modes are excited. Tone loudness affects the phase difference in the French horn. Although louder tones of the same mode seem to yield larger absolute values of the phase difference, 5th and 11th modes go against this tendency. From the result of Fig. 7, we may qualitatively conclude the following: The outward-striking lip model is applicable to the lowest second mode; the upward-striking model predominates at other higher modes.

III. DISCUSSION

A. Waveforms of mouthpiece pressure and lip strain

FIG. 7. Measured phase difference between the mouthpiece acoustic pressure p and the player's lip strain ε in the trumpet and French horn. Gauge B2 was used for strain detection.

Figure 8 displays waveforms of the mouthpiece pressure p and of the lip strain ε for four notes played on a French horn. The notes are played in about mf though the F3 note is close to f. The absolute magnitude of the mouthpiece pressure is determined from the internal 50-mV reference of the amplifier (B&K type 2609) and the nominal sensitivity (3.16 mV/Pa) of the probe microphone. That of lip strain is determined by an internal reference which can be set up arbitrarily.
Since pressure and strain signals are digitally sampled at the rate of 1 ms, the waveforms in Fig. 8 are not so smooth as those measured with an analog oscilloscope. Nevertheless, Fig. 8 shows the characteristic common to brass instruments : The mouthpiece pressure of low-pitch notes is virtually non-sinusoidal, while that of higher-pitch notes is nearly sinusoidal.5,24 On the other hand, there are no previous ex perimental results with which to compare the strain waveform. According to Fig. 8, the strain waveform changes from non sinusoidal for low-pitch notes to nearly sinusoidal for higher-pitch notes, just as the pressure waveform does. However, the strain waveform does not follow the pressure waveform, particularly for low-pitch notes.
Also, in contrast to the quasi sinusoidal lip vibration,4 the lip strain is non sinusoidal. This non sinusoidality might depend on the time interval during which the lips close. For example, the strain waveform for C3 appears to show the lips closing for about one third of the cycle (remember that a positive strain corresponds to a negative displacement as discussed in Section I C). This closing time interval appears to diminish for higher-pitch notes and consequently the strain waveform approaches sinusoidality. However, more experimental data is needed to construct a definitive explanation for this interesting difference between displacement and strain waveforms.

B. Sounding frequency versus resonance frequency

FIG. 8. Measured waveforms of mouthpiece pressure and lip strain for the notes F2, G3, F3, and A3 played in mf level on the French horn.

The relation between the sounding and passive resonant frequencies can decisively indicate whether the oscillation is based on the outward-striking lip or the upward-striking lip. Therefore in this subsection the calculated resonance frequencies of lip-driven pipes and mouthpiece-resonant tube systems are compared with their sounding frequencies. Such a comparison will give a good reconfirmation of the results from the phase-difference measurements.
A cumbersome problem in calculating the resonance frequency is the mean temperature which determines the average speed of sound in the above-mentioned acoustical systems. Elliott and Bowsher5 carefully estimated the temperature distribution to derive the correct intonation of the trombone, based on the following measurement of Wogram:34 The temperature falls almost exponentially from about 33 at the mouthpiece, to 26 halfway down the instrument, to 24°C (room temperature) at the bell. In our case of simple cylindrical geometries for resonance, the mean temperature may be roughly approximated by the arithmetic mean of the mouthpiece (or pipe input) temperature (about 33°C) and the room temperature (about 21 °C), that is, 27°C. This mean temperature yields the average sound speed of 347.4 m/s.35
First let us calculate the resonance frequencies of pipes 1 and 3 (cf. Section II A). Their acoustical lengths are 291.3 and 293.8 mm, respectively, where the end correction is given as 0.62 x (pipe radius). The player's lips, which protrude into the pipe, hardly affect this acoustical length because the cross-sectional area of the pipes is much larger than the lip area. The resonance frequencies of pipes 1 and 3 are then 298.1 and 295.6 Hz, respectively. If this resonance frequency is marked in Fig. 3, one can understand that the outward-striking oscillation occurs above the resonance and the upward-striking oscillation occurs below the resonance. This result on the frequency relation agrees with the result on the phase relation of Fig. 3 very well, and indicates the reliability of our phase-difference measurement method.
Next let us consider the effects of the mouthpiece on the resonance. Figure 9(a) shows an equivalent electrical circuit for the brass instrument consisting of a player, a mouthpiece, and a horn. A constant driving pressure P0 at the player's lung is applied to the mouthpiece through the player's trachea, mouth, and lip opening. For low mode oscillations Fig. 9(a) can be simplified to Fig. 9(b) because the time-varying resistance Rs(t) and inductance Ls(t) of the lip opening are negligible compared with the magnitude of the impedance Zh of the horn.5,24 As a result, the capacitance CM of the mouthpiece cup couples with the capacitance Cm of the player's mouth. Since the strength of this coupling is not easily estimated, the player side represented by the lung capacitance C0, the trachea inductance L0, and the mouth capacitance Cm in Fig. 9(a) is simplified to the equivalent capacitance C'm in Fig. 9(b).
The circuit of Fig. 9(b) is applicable to the calculation of the resonance frequency of tube Rl with a mouthpiece (cf. Section II C). A mathematical expression of Zh for real brass instruments is not available, but that for a cylindrical tube is given as

Zh = jZ0 tan kl,       (4)

where Z0 is the characteristic impedance, k the wave number, and l the acoustical length. For simplicity, the energy dissipation in the tube is neglected in Eq. (4). The resonance frequency of the circuit of Fig. 9(b) is given by the maximum of the input impedance Zm as seen from the player's mouth as follows

1/Zin = 1/(Zh + jωLM) + jωC = 0,       (5)

where

(the coupled capacitance) C = CM + C'm = V / ρc²       (6)

(the throat inertance) LM = ρlM /SM        (7)

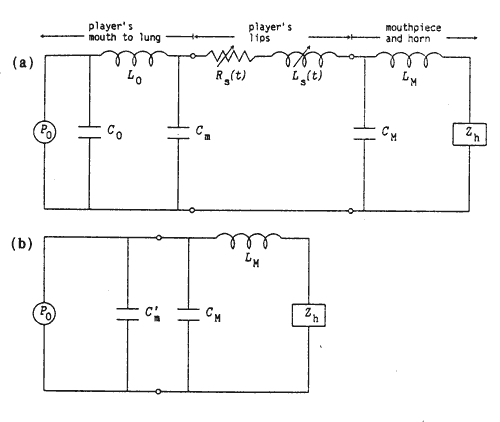
FIG. 9. Equivalent electrical circuit: (a) equivalent circuit for brass instru­ments, (b) simplified circuit for brass instruments in low mode oscillation and for mouthpiece-resonant tube systems, where the coupling between the mouthpiece cup and the player's mouth is assumed.

In Eq. (6) V denotes the effective coupled volume of the mouthpiece cup and player's mouth when the player adjusts the embouchure, ρ the air density, and c the average sound speed (= 347.4 m/s). In Eq. (7) lM and SM are the length and cross-sectional area of the mouthpiece throat, respectively. Since Z0 is given as ρc/S (S: the cross-sectional area of the tube), Eq. (5) can be rewritten as

tan kl = (lS / V)(1 / kl) – (lM / l)(S / SM) kl       (8)

using Eqs. (4), (6), and (7). Table I shows the geometries of the French horn mouthpiece- and trumpet mouthpiece-resonant tube Rl systems. Figure 10 shows the resonance frequency fres (= ck /2π) calculated from Eq. (8) and Table I.
In Fig. 10 fres is given as a function of the coupled cavity volume V. The cup volume of a mouthpiece is reduced by an amount equal to the volume displaced by the player's lips pressed against the rim. For example, the displaced volume was estimated as 2.5 ± 0.5 cm3 for the cup volume 4.7 cm3 of the trombone mouthpiece.22 This displaced volume is roughly estimated as 1.5 for the French horn, and as 0.5 cm3 for the trumpet (see solid lines in Fig. 10). The cup volume is then reduced to 1.4 for the French horn, and to 1.0 cm3 for the trumpet. The cup volume may be further reduced by embouchure under instrument playing conditions. The smallest cavity volume is assumed to be 1.0 for the French horn, and 0.5 cm3 for the trumpet (see solid line in Fig. 10). A protruding embouchure, which results in a larger lip opening, is probably a major factor in the coupling of the player's mouth cavity with the cup cavity. The largest cavity volume is assumed to be 3.0 cm3 for both the French horn and the trumpet under playing conditions, and we obtain almost the same resonance frequency width as shown in Fig. 6.

TABLE I. Geometry of mouthpiece-resonant tube system

		French horn mouthpiece-resonant tube R1	Trumpet mouthpiece-resonant tube R1
Acoustical tube length	l (mm)	346	370
Tube radius	a (mm)	3.5	3.5
Mouthpiece throat length	lM (mm)	40	74
Mouthpiece throat radius	aM (mm)	3.1	4.2
Mouthpiece cup volume	VM (cm3)	2.9	1.5

FIG. 10. Resonance frequency fres of mouthpiece-resonant tube systems as a function of the cavity volume V due to the coupling between the mouth­piece cup and the player's mouth. •: French horn mouthpiece and resonant tube Rl. ♦: Trumpet mouthpiece and resonant tube Rl. The solid line in­dicates the assumed range of the cavity volume under blowing conditions.

These calculated resonance frequencies shown by the solid lines in Fig. 10 are clearly lower than the sounding frequency shown in Fig. 6. This result in the frequency relation, which corroborates the result on the phase relation of Fig. 6, indicates an outward-striking oscillation. Therefore we may consider that the mouthpiece reduces the lip flexibility displayed in lip-driven pipes and brings out only the outward-striking oscillation for the first of mouthpiece-resonant tube systems through the player's mouth-mouthpiece cavity coupling.

C. Outward-striking oscillation versus upward-striking oscillation

Major questions arising from Fig. 7 on the phase difference Lp – Lξ in the French horn and trumpet are the following:
(1) How is the transition from the outward-striking oscillation in low modes to the upward-striking oscillation around the third mode determined ?
(2) What produces the much larger values of Lp – Lξ in higher modes (above the eighth) of the French horn ?
The first question seems to be related to the drastic change in tone waveform when the oscillation shifts from the lowest (second) mode to higher modes. This change essentially depends on the relative magnitudes Rs /|Zh| and Ls /|Zh| in Fig. 9.5,24 For low modes, Rs and Ls are negligible compared with |Zh| as shown in Fig. 9(b). Therefore, the oscillation and waveform are determined by the input impedance Zin defined by Eq. (5). This Zin should be capacitive for the second mode oscillation of the French horn and the trumpet as inferred from the results shown in Fig. 10 on first mode oscillations of mouthpiece-resonant tube systems because their phase difference Lp – Lξ is negative as shown in Fig. 6. The outward-striking oscillation is supported by the capacitive input impedance. This capacitiveness of Zin may be controlled by the C of the coupled mouth-mouthpiece cavity.
However, such direct cavity coupling is cut off as shown in Fig. 9(a) when the resistance Rs and inductance Ls of the lip opening become dominant in higher mode oscillations. As a result, the input impedance Zin as seen from the player's mouth tends to be inductive because of the small effect of the horn impedance Zh [numerical calculation of the circuit shown by Fig. 9(a) as a function of the frequency is necessary in the future, though]. This situation is likely to yield the upward-striking oscillation and the more sinusoidal waveforms that mainly depend on nonlinear impedance of the narrow lip opening. Hence the transition between oscillation regimes, which corresponds very closely to the transition between tone waveforms, will be determined by mouth-mouthpiece decoupling due to the impedance of the narrow lip opening.
Also, a narrow lip opening produces the Bernoulli effect. Although this effect depends on the flow separation mode at the lip opening and this flow condition is not known exactly, we may postulate its existence just as in the case of vocal-cord vibration.9,10,25,26 The time-varying pressure ps(t) arising from a reduction of pressure at a narrow opening is given by

ps(t) = –ρUv(t)       (9)

in a linear approximation, where U and v(t) are the mean flow velocity and the time-varying flow velocity, respectively. In deriving Eq. (9) we assumed that the pressure at the opening Ps can be approximated by P0 – (1/2)ρ(U + v)2, where P0 is the constant blowing pressure.9 Therefore the magnitude of ps(t), which yields the upward motion, generally increases as the blowing pressure increases. On the other hand, since the mouthpiece pressure generally decreases for ascending modes,20 the upward-striking oscillation tends to be dominant for higher mode tones in brass instruments.
It should be noted that the time-varying pressure ps(t) of Eq. (9) acts on a lip area A parallel to the flow direction, while the mouthpiece pressure acts on the lip area A¹ perpendicular to the flow direction. Therefore the ratio of A/A¹ seems to be another possible cause for the oscillation transition. This ratio changes according to lip configuration, which depends on the blowing pressure and on player's embouchure. Higher blowing pressures are likely to make the ratio larger than one in spite of the decreasing lip thickness due to the increasing elastic tension necessary to raise the resonance frequency of the lip. This tendency is shown in the euphonium.6 Using observed values of the effective lip breadth b and the effective lip thickness d, and using the value of effective lip height h (estimated by assuming the validity of their theory36), Saneyoshi et al.6 evaluated A = (bd /2) and A¹ (= bh). According to Table IV of Ref. 6, A¹ is slightly larger than A for the lowest note Bbl, but A is larger than A¹ for the other higher notes. We may infer from the result of Fig. 7 that a similar situation probably applies to the French horn and the trumpet.
Also, they predicted the phase difference Lp – Lξ from the measured playing frequency and its rate of depression to the nominal frequency of mode tone [cf. Eq. (44) and Fig. 6 of Ref. 6]. According to their results, the phase difference in the euphonium is relatively large and increases from about 15° to 50° as the note played ascends from the first mode (Bb1) to eighth mode (Bb4). This prediction seems to qualitatively match that seen in Fig. 7, although the lowest, second mode of the French horn and trumpet supports the outward-striking oscillation. This agreement suggests the experimental verification of their theory.
For the lowest mode case of lip-driven pipes without a mouthpiece, the player's lips can make full use of their flexibility to change the area ratio A/A¹ over a wide range. In this case two oscillation regimes may appear in this system in spite of low blowing pressures. However, lip flexibility is checked by the mouthpiece rim. Therefore only the outward-striking oscillation is likely to appear in nonresonant and resonant tubes with a mouthpiece when the lowest mode tone is produced by low blowing pressures.
Until now we have considered the following three candidates for the oscillation transition in the French horn and trumpet : (1) the player's mouth-mouthpiece decoupling, (2) the Bernoulli effect at a narrow lip opening, and (3) the ratio A/A¹ in the vibrating lip configuration. A self-consistent explanation of the oscillation transition from these three requires at least tissue mechanics to illustrate that the increasing elastic tension necessary to raise the lip resonance frequency yields a narrower lip opening (=bξ) and a larger value of A/A¹ (=d /2h) simultaneously. Further investigations are necessary to construct a more definite and quantitative description on the oscillation transition and to reveal the actual cause of the transition.
Still there remains the question mentioned in item (2) in the first paragraph of this subsection. It seems that the values of Lp – Lξ above the eighth mode in the French horn are too large to sustain self-oscillation, if we assume that there is no phase difference between the lip displacement and the acoustic volume velocity which drives the instrument. Let us therefore postulate that the time-varying flow velocity at the lip opening v(t) is proportional to the velocity of the upper lip when it closes, just as in the vocal-cord oscillation:9 v = –α(dξ/dt), where α denotes a positive constant. Therefore from Eq. (9) we have

ps = αρU (jωξ).       (10)

Since the acoustic pressure in the mouthpiece p is approximated by ps,5,6 Eq. (10) implies that there will be a 90° phase difference between p and ξ if the brass player's lips self-oscillate exactly like one-mass vocal cords.
Hence we may consider that there is large possibility that upward-striking oscillation exists in higher modes above the eighth in the French horn. This hypothesis is mainly derived from the air inertance and resistance at the lip opening, but the details of the phase difference are affected by the acoustic pressure in player's mouth,5 the fluid-dynamical situation around the lips,37 the resonance characteristics of the instrument, tone loudness, etc. Also, the author has persisted in one-dimensional models (outward-striking lip and upward-striking lip) to focus on their fundamental aspects. A more comprehensive explanation on the self-oscillation of brass player's lips might be obtained if we took more flexible two-dimensional lip models15,16,19 or two-mass vocal-cord models25,26 into proper consideration. Nevertheless, within the scope of the above discussions we may conclude that the self-oscillation in brass instruments varies from the outward-striking oscillation to the upward-striking oscillation with ascending tone mode.

IV. CONCLUSIONS

The acoustical behavior of brass player's lips was investigated in experiments on four types of acoustical systems : lip-driven pipes without a mouthpiece, a non resonant tube with a mouthpiece, resonant tubes with a mouthpiece, and real brass instruments. The prime question was whether the player's lips self-oscillate in an outward-striking mode or in an upward-striking mode. Measurement of the strain of the vibrating upper lip instead of the particle velocity near the lips was carried out because of practicality and ease of strain detection under playing conditions. The phase difference between the mouthpiece pressure and the lip displacement was derived from the pressure-strain phase difference and was calibrated from the near-field pressure of a vibrating convex diaphragm on which a strain gauge was secured. Postulating that this phase difference changes in a manner similar to the input impedance phase around the passive resonance of the system, a negative / positive value for this phase difference suggests outward-striking / upward-striking oscillation of the lips.
The experimental results revealed the following:
(1) Larger lip-driven pipes support both outward-striking and upward-striking oscillations because of lip's high flexibility to form various embouchures. However, a small lip-driven pipe hardly supports the outward-striking oscillation.
(2) Mouthpiece-non resonant tube systems almost support the outward-striking oscillation over a wide frequent range. The behavior of the buzzing lips seems to be reflected by this acoustical system.
(3) Mouthpiece-resonant tube systems totally support the outward-striking oscillation. These systems have a much wider frequency bandwidth of resonance than lip-driven pipes without a mouthpiece do.
(4) The French horn exhibits the outward-striking oscillation for the lowest (second) mode and the upward-striking oscillation for other higher modes. In the trumpet the second and fourth mode tones are sustained by the former and the latter, respectively, and both are mixed for the third mode oscillation.
The resonance frequency was calculated and compared with the sounding frequency for the reconfirmation of the above results (1) and (3). This result, which indicates that the outward-striking/upward-striking oscillation occurs above/below the resonance, demonstrated the reliability of the phase-difference measurement method. Moreover, the hypothesis of a player's mouth-mouthpiece cavity coupling in the lowest mode plausibly explained the wide resonance bandwidth mentioned in (3). This hypothesis may be justified by the negligible magnitude of the lip-opening impedance compared with the tube input impedance.5,24
A strong correlation was seen between the oscillation regime and the waveform in the French horn and trumpet : The mouthpiece pressure of low-pitch notes, particularly of the second mode tone, is very non sinusoidal and sustained by the outward-striking oscillation; that of higher-pitch notes is more sinusoidal and sustained by the upward-striking oscillation. We believe that the oscillation regime and waveform regime transitions depend on the magnitude of the lip-opening impedance. If this impedance is negligible in comparison with the input impedance of the instrument as seen from the player's mouth, cavity coupling between player's mouth and mouthpiece cup will occur and yield a capacitive input impedance that favors the outward-striking oscillation. This situation is very similar to the above item (3).
On the other hand, if the magnitude of the lip-opening impedance becomes comparable with that of the input impedance as the blowing pressure increases, cavity decoupling will result in an inertive input impedance that favors the upward-striking oscillation. Since the time-varying Bernoulli pressure at the lip opening and the lip area receiving this pressure are apt to increase as the blowing pressure increases, the upward-striking oscillation tends to be predominant for higher mode tones in brass instruments. The pressure-displacement phase difference approaches 90° when a mode above the eighth is selected. This experimental result suggests that the brass player's lips self-oscillate exactly like one-mass vocal cords for such higher modes. Fundamental aspects in a brass player's lip function have been made clear by the present work. As a result, we may comment that it is essential that brass players should practice not buzzing the lips but controlling lip flexibility to achieve accurate mode selection. In this sense, a non resonant tube for the buzzing practice is dispensable because a non-resonant tube supports the outward-striking oscillation which cannot produce the higher-pitch notes in brass instruments. For a more detailed analysis of the sounding mechanism and mode selection in brass instruments, the coupling and decoupling between the player's mouth and mouthpiece by the lip opening must be understood more exactly, particularly from the fluid-dynamical viewpoint.

ACKNOWLEDGMENTS

The author thanks Professor George R. Plitnik of Frostburg State University for suggesting the experiment on a nonresonant tube and for his support of the experiment on the trumpet. The author also expresses thanks to Hiroyuki Ohtsuki of the ATR Human Information Processing Research Laboratories for playing the French horn and to Dr. Seiji Adachi of ATR for his help in the French horn experiment and for his comments on the manuscript. The author is grateful to Dr. James B. Cole of the U.S. Naval Research Laboratory (temporarily of the Research Institute of Electrical Communication, Tohoku University, Japan) for his careful editing of the English expression. The author also thanks Professor Thoru Idogawa of Saitama Institute of Technology and Professor Keinosuke Nagai of Tsukuba University for their long-term support of these experiments. Finally, the author would like to express his acknowledgments to the anonymous reviewers, each of whom contributed relevant comments and valuable suggestions.

1H. L. F. Helmholtz, On the Sensations of Tone, translated by A. J. Ellis (Dover, New York, 1954), pp. 95-102.
2N. H. Fletcher, "Excitation mechanism in woodwind and brass instruments," Acustica 43, 63-72 (1979); 50, 159(E) (1982).
3N. H. Fletcher, R. K. Silk, and L. M. Douglas, "Acoustic admittance of air-driven reed generators," Acustica 50, 155-159 (1982).
4D. W. Martin, "Lip vibrations in a cornet mouthpiece," J. Acoust. Soc. Am. 13, 305-309 (1942).
5S. J. Elliott and J. M. Bowsher, "Regeneration in brass wind instruments," J. Sound Vib. 83, 181-217 (1982).
6J. Saneyoshi, H. Teramura, and S. Yoshikawa, " Feedback oscillations in reed woodwind and brasswind instruments," Acustica 62, 194-210 (1987).
7S. Yoshikawa, " Self-oscillation of brass instruments viewed from one-mass vocal cord vibration," Proceedings of the Spring Meeting of the Acoustical Society of Japan, pp. 379-380 (1987).
8S. Yoshikawa, "On the modeling of self-oscillation in brass instruments," J. Acoust. Soc. Am. Suppl. 1 84, S161 (1988).
9I. R. Titze, "The physics of small-amplitude oscillation of the vocal folds," J. Acoust. Soc. Am. 83, 1536-1552 (1988).
10K. Ishizaka and M. Matsudaira, " Fluid mechanical considerations of vocal cord vibration," Monograph No. 8, Speech Communications Research Laboratory, Santa Barbara, CA (1972).
11I. R. Titze and D. T. Talkin, "A theoretical study of the effects of various laryngeal configurations on the acoustics of phonation," J. Acoust. Soc. Am. 66, 60-74 (1979).
12M. E. Mclntyre, R. T. Schumacher, and J. Woodhouse, "On the oscillation of musical instruments," J. Acoust. Soc. Am. 74, 1325-1345 (1983).
13D. H. Keefe and M. Park, " Tutorial on physical models of wind instruments: II, Time domain simulations," Tech. Rep. Ser. No. 9002, School of Music, University of Washington, 1990.
14D. H. Keefe, "On sound production in brass instruments," J. Acoust. Soc. Am. Suppl. 1 87, S138 (1990).
15W. J. Strong, "Computer simulation of a trumpet," J. Acoust. Soc. Am. Suppl. 1 87, S138 (1990).
16W. J. Strong and J. D. Dudley, "Simulation of a player- trumpet system," Proceedings of the Stockholm Musical Acoustics Conference (unpublished).
17G. A. Redhead, "Toward a model of sound production in the trumpet for musical synthesis," Report, Department of Electrical and Electronic Engineering," University of Canterbury, Christchurch, New Zealand, 1993.
18S. Adachi and M. Sato (unpublished).
19S. Adachi and M. Sato, " Brass instrument simulation using a lip vibration model with two degrees of freedom," Tech. Rep. of the IEICE, No. EA94-25, 1994.
20J. D. Dudley and W. J. Strong, "A computer study of the effects of har-monicity in a brass wind instrument : Impedance curve, impulse response, and mouthpiece pressure with a hypothetical periodic input," Appl. Acoust. 30, 117-132 (1990).
21J. Backus, " Input impedance curves for the brass instruments," J. Acoust. Soc. Am. 60, 470-480 (1976).
22S. Elliott, J. Bowsher, and P. Watkinson, " Input and transfer response of brass wind instruments," J. Acoust. Soc. Am. 72, 1747-1760 (1982).
23R. Causse, J. Kergomard, and X. Lurton, " Input impedance of brass musical instruments-Comparison between experiment and numerical models," J. Acoust. Soc. Am. 75, 241-254 (1984).
24J. Backus and T. C. Hundley, " Harmonic generation in the trumpet," J. Acoust. Soc. Am. 49, 509-519 (1971).
25K. Ishizaka and J. L. Flanagan, "Synthesis of voiced sounds from a two-mass model of the vocal cords," Bell Syst. Tech. J. 51,1233-1268 (1972).
26I. R. Titze, "On the mechanics of vocal-fold vibration," J. Acoust. Soc. Am. 60, 1366-1380 (1976).
27N. H. Fletcher, "Autonomous vibration of the simple pressure-controlled valves in gas flows," J. Acoust. Soc. Am. 93, 2172-2180 (1993).
28S. Yoshikawa and G. R. Plitnik, "An experimental investigation of the phase difference between lip vibration and acoustic pressure in brass instrument mouthpieces," J. Acoust. Soc. Am. 94, 1834(A) (1993).
29S. Yoshikawa and G. R. Plitnik, "A preliminary investigation of brass player's lip behavior," J. Acoust. Soc. Jpn. (E) 14, 449-451 (1993).
30P. M. Morse, Vibration and Sound (McGraw-Hill, New York, 1948), 2nd ed., pp. 312-313.
31H. W. Henderson, "An experimental study of trumpet embouchure," J. Acoust. Soc. Am. 13, 58-64 (1942).
32R. D. Weast, "A stroboscopic analysis of lip function," The Instrumentalist 23, 44-46 (1963).
33Technical terms like outward-striking reed model and one- mass vocal-cord model have been abandoned at this point because "lip" models are now considered. The outward-striking reed is replaced with the outward-striking lip, the one-mass vocal cord with the one-mass upward-striking up.
34K. Wogram, "A contribution to the measurement of the intonation of brass instruments," Ph.D. thesis, Technische Universitat Carolo-Wilhelmina, Braunschweig, 1972.
35L. L. Beranek, "Acoustic properties of gases," A merican Institute of Physics Handbook (McGraw-Hill, New York, 1963), 2nd ed.
36As Fletcher27 pointed out properly, the concept of a reed striking inward seems to be physically inapplicable to the lip-driven brass instruments. A non-outward-striking reed was carelessly considered as the inward-striking reed in Ref. 6 because the time-varying Bernoulli pressure in the vocal-cord model is approximated by the acoustic pressure in the mouth piece. However, as Fig. 2 of Ref. 6 displays, the physical model adopted in Ref. 6 is essentially a perpendicular model similar to that shown in Fig. l(c) of Ref. 27, which is representing the lip motion perpendicular to the blowing flow. In this context, the concepts of reed striking inward and reed striking outward should be categorized as a parallel model, where the reed vibrates parallel to the flow direction.
37A. Hirschberg, R. W. A. van der Laar, J. P. Marrou- Maurieres, A. P. J. Wijsnands, H. J. Dane, S. J. Kruijswijk, and A. J. M. Houtsma, "A quasi-stationary model of air flow in the reed channel of single-reed woodwind instruments," Acustica 70, 146-154 (1990).