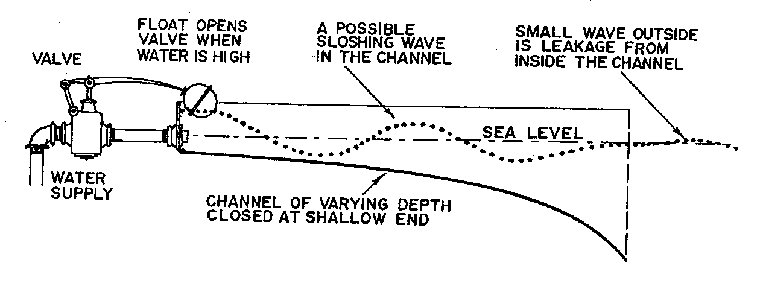
Figure 2: The "water trumpet"
Water waves moving in an open channel of varying cross section obey precisely the same equations as do the sound waves that oscillate in an air column of varying cross section. The channel is therefore an easily visualized model of the instrument's air column. The lengthwise swinging of air in the column is replaced by the lengthwise sloshing of the water in the channel, and our lips and lungs are replaced by a flow-control valve conned to the city water supply. Figure 2 shows this hypothetical water trumpet, which is analogous to our familiar musical instrument.

Figure 2: The "water trumpet"
In this machine we will assume that a float valve is controlled by the varying height of the water at one end of a sloping channel, the other end of which communicates with the open sea. The valve is so arranged that it squirts a short burst of water into the channel whenever the water level here is high enough, and shuts off, or at any rate reduces, the flow whenever the water falls below this critical level. If one were to set up a sloshing of water in the channel, and if the sloshing were strong enough to trip the valve open at its peaks, the valve would be opening and shutting in time with the sloshing--a set-up that conceivably might maintain this back-and-forth swinging of water waves indefinitely.
By striking a skillet with a spoon, an iron bar with a mallet, a piano string with a hammer, or the end of an air column with a sharp slap of the hand, one can set into a complex vibration the skillet, the bar, the string, or the air column. This complex vibration is made up of a set of building-block vibrations, each of which has its own characteristic motion and its own particular defined frequency. The strength of the vibration of each of these vibrational modes depends on the place and manner in which the impulsive excitation is applied, as well as on its own vigor; but the frequencies at which these vibrations take place are solely determined by the object that has been struck. These characteristic frequencies, which are also called the natural frequencies of the object in question, are not necessarily members of a harmonic series, nor do they necessarily have any other orderly progression. These general remarks about natural vibrations apply perfectly well to the sloshing of water up and down our channel if they are all caused by a single impulse of water entering through a momentary opening of the valve.
Suppose now that in our initial investigation of the water trumpet, we select a particular taper for its channel and see whether it could properly instruct the valve (which fulfills the function of our lips on an actual trumpet) so as to make possible a sustained type of oscillation (such as is possible also when a bow interacts with a musical string, or when a woodwind player blows on his instrument). This sustained oscillation, which lasts until the player's lungs are deflated, is quite distinct in its nature from the impulsively started natural vibrations that must inevitably die away due to the effects of friction, as they do in the case of a struck skillet, bar, or piano string. Let our channel have a curving bottom arranged so that the water is very shallow at the closed ("mouthpiece") end where the valve acts, and fairly deep at the end that is open to the sea. Let us suppose for simplicity that the channel is of such length and depth that the natural mode of oscillation having the lowest frequency is one for which the sloshing recurs once each second. If this were the only mode of oscillation, it by itself would then be asking the valve to admit a burst of water at one-second intervals. So far so good, but what about the second mode of water oscillation it is possible to have in this channel? One might have (to choose a specific example) a channel having such rate of taper that the second natural mode of swinging takes place 2.25 times per second, so that it would call on the valve to inject pulses of water this many times per second. In a channel of this shape, the third mode of oscillation would like to keep things running at 3.58 repetitions per second, the fourth would prefer 4.87 per second, and so on.
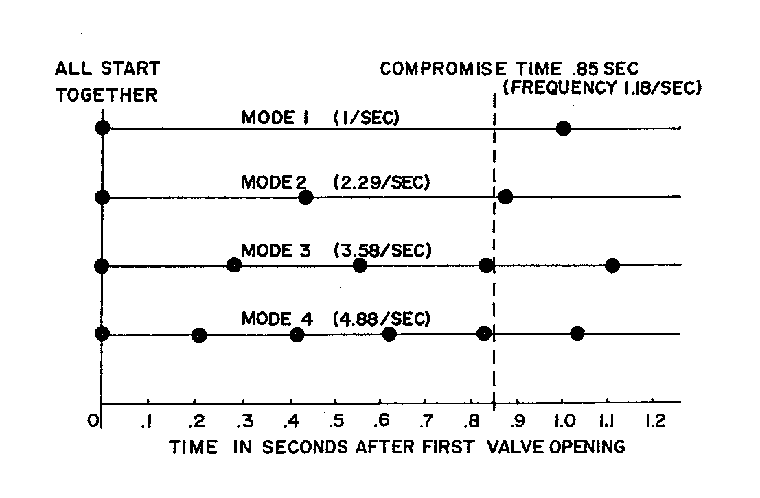
Figure 3: Schedule of valve openings for the first four modes
The first injected pulse of water acts like a piano hammer to excite the sloshing modes characteristic of the water in the channel. The question then arises concerning the moment when the second pulse should take place if it is to keep all of these modes going. The top line of Fig. 3 shows by black dots the instants, one second apart, at which the valve should open to sustain the lowest frequency oscillation of the water. The second line similarly shows what is needed by the second mode, and so on. All the swinging are started together in our channel at the first burst of fluid injected, but they get into a quarrel very quickly about how soon the wave should inject its next little slug of water. We see that while mode 1 would like the valve opened after exactly 1 second, mode 2 votes to open it early at about 0.87 seconds, and mode 3 would prefer to have water injected at 0.84 seconds. Mode 4 is a different sort of troublemaker--it would be equally happy to have a burst quite early, at 0.82 seconds, giving a push to its fourth swing, or a trifle late at 1.02 seconds, in time with its fifth swing. Since all of these separate sloshings must cooperate in order to pile up the water high enough to open the valve, we find that our sloping water channel would not find it easy to maintain a steady oscillation. If on the other hand the float does not have to be raised too much in order to open it, then only a partial cooperation will be needed among the modes. Under these conditions a certain type of oscillation is possible in the channel. The system could find a workable compromise time at about 0.85 seconds, which corresponds to an overall repeating frequency of 1.18 sloshings per second. Interestingly enough, this frequency has no simple relation whatever to any of the channel's natural frequencies, although it is chiefly influenced by modes 2, 3, and 4. The oscillation is however sustained by a certain degree of cooperation among all of them.
Another kind of oscillation that might be imagined in this water trumpet is one in which mode 1 swings in step with every fifth swing of mode 4, modes 2 and 3 being left out of the game. It turns out however that oscillations of this type are not usually possible because of certain anti-cooperative effects arising from the ignored modes. We find examples of all these phenomena throughout the world of wind instruments, and we shall meet practical versions of several of them in later part of this chapter.
Our introductory meeting with the sloshing modes of vibration of water in an open channel gives us an initial idea of the musical importance of the acoustical theory of waves in a channel of varying width, and of the technical understanding of the way a flow-control device can cooperate with an air column to maintain oscillations within it. Certain mechanical requirements must be met if sound is to be produced at all, and more stringent requirements are laid on us if we wish to produce dependable and pleasant sounds. The beginnings of a scientific understanding of these matters occurred many years ago, and we are in a position now to turn away from our metaphorical water trumpet and take up a few items of acoustical history. Let us begin with the flow-control aspect of sound production in wind instruments.
Trumpet Acoustics
Acoustical Preliminaries
The "Water Trumpet"-- An Analog to What Happens inside a Trumpet
The Function of the Player's Lips
The Function of the Pipe and Bell--Inside the Air Column
The Cooperation Needed for Musical Results
The Baroque Trumpet
The 'Internal' Spectrum of the Modern Trumpet
The 'Internal' Spectrum of the Baroque Trumpet
Relation of Internal to External Tone Color Spectrum
The Menke Trumpet
The Problem of Clean Attack
Mahillon in Retrospect
Conclusion
Bibliographic Notes